Paraboloide

---

Paraboloide

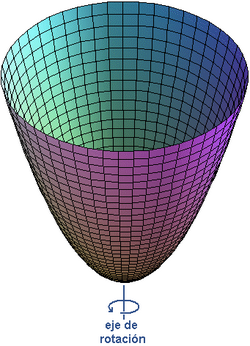
El paraboloide es, cuando no se precisa, un paraboloide de revolución, es decir la superficie generada por la rotación de una parábola alrededor de su eje de simetría (ver figura a la derecha).

Si se escoge como sistema de coordenadas

$(O,{\vec {i}},{\vec {j}},{\vec {k}})$

, donde O es el vértice de la parabola,

${\vec {k}}$

un Vector director del eje de simetría (tanto de la parabola como del paraboloide), y

$({\vec {i}},{\vec {j}})$

una base del plano perpendicular al eje, entonces la ecuación de la superficie es:

$z=a\cdot (x^{2}+y^{2}),\quad a\neq 0$.

Esta ecuación proviene de la de la parábola: y = a·x² donde se ha remplazado y por z porque la parábola que genera la paraboloide es vertical ("de pie"), y luego se remplaza x² por x² + y² para incluir la tercera dimensión (el eje de las ordenadas es horizontal como él de las abscisas y tiene el mismo papel). Así la parábola de referencia y = x² genera por rotación el paraboloide z = x² + y².

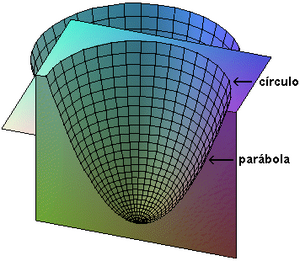
La intersección del paraboloide anterior por un plano vertical (es decir paralelo al eje de simetría) se obtiene logicamente una parábola, mientras que si se corta por un plano horizontal (ortogonal al eje mensionado) se obtiene un círculo (ver figura a la izquierda).

El paraboloide comparte con su análoga bidimensional la parábola la propiedad del punto focal: Todos los rayos paralelos al eje, al tocar la superficie son reflejados y convergen en un único punto llamado foco. Este principio es utilizado por las llamadas «antenas parabólicas» que de hecho son paraboloides, ya que en el foco se encuentra el receptor de ondas.
Inversando el sentido de las mismas se obtiene el principio del faro: una fuente de luz situada en el foco emite rayos que, al ser reflejados el el espejo en forma de paraboloide dan un haz de luz paralelo, que por tanto no se dispersa y es visible a gran distancia.
La distancia focal, es decir la que separa el foco del vérice, es, para el paraboloide de ecuación z = a·(x² + y²),

$d={\frac {4}{a}}$

. Cuanto más llano es paraboloide (menor es el parámetro a) más lejos se encuentra el foco.

El volumen comprendido entre la superficie y el plano situado a la altura h (plano de ecuación z = h) es ${\frac {S\cdot h}{2}}={\frac {\pi \cdot a^{2}\cdot h}{2}}$, donde S es el área del círculo de intersección.
Si uno se aproxima al vértice del paraboloide, mirándola con una lupa o un microscopio, verá su superficie aplanarse, lo que significa que un cambio de escala equivale a modificar el valor del párametro a. Esto permite afirmar que, mediante cambios de escala, y claro, rotaciones y translaciones, en esencia sólo existe un único paraboloide por ejemplo la de ecuación z = x² + y².

El paraboloide es una cuádrica, es decir una superficie definida por un polinomio de segundo grado. Las cuádricas se clasifican, y las en donde una de las variables aparece en forma lineal (con el grado uno) y las otras dos en forma cuadrática (con el grado dos) se llaman también , por generalización, paraboloides (aunque no de revolución).

Eligiendo el sistema de coordenadas adecuado, la ecuación será de la forma:

$z=A\cdot x^{2}+B\cdot y^{2}$

, donde se puede imponer A > 0 (cambiando z por -z si hace falta).
Si B es también positivo, se pone

$A={\frac {1}{a^{2}}},B={\frac {1}{b^{2}}}$

, y la ecuación será:

$z={\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}$

Se llama paraboloide elíptico a esta superficie, porque las secciones por los planos horizontales (z = k ) son elipses (de ecuación ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=k$, sus semiejes son k·a y k·b ) en vez de círculos como en el paraboloide de revolución, pero sus secciones por planos verticales siguen siendo parábolas. No se ha representado esta superficie por ser de aspecto muy similar a la figura anterior (bastaría con alargarla en una dirección horizontal).

Si B es negativo, se pone

$A={\frac {1}{a^{2}}},B=-{\frac {1}{b^{2}}}$

, y la ecuación será:

$z={\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}$

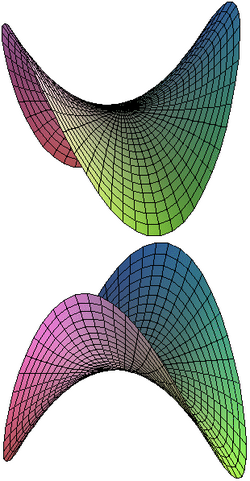
Se llama paraboloide hiperbólico a esta superficie (no confundir con los hiperboloides), representada según dos puntos de vista distintos en la figura a la derecha: en una dirección (en el plano y = 0) presenta el aspecto de una parábola orientada hacia arriba (de ecuación

$z={\frac {x^{2}}{a^{2}}}$

 ), y en otra dirección perpendicular (en el plano x = 0) la de una parábola orientada hacia abajo (de ecuación

$z=-{\frac {y^{2}}{a^{2}}}$

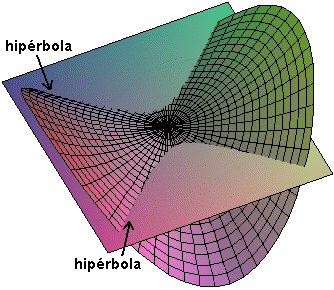
 ). Las secciones por planos horizontales son hipérbolas - lo que justifica su apelación - como queda representado en la figura abajo.

Se llama también silla de montar a esta superficie, o puerto de montaña. Es una forma fundamental en la topología, y el vértice (el origen) tiene la propiedad de ser un máximo de la función

$f(x,y)={\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}$

cuando y varía, y un mínimo de la misma cuando x varía. Este punto es por tanto a la vez un máximo y un mínimo, un «minimax». En la teoría de los juegos representa un punto de equilibrio, y muchas teorías en economía utilizan el minimax (un agente económico impone el valor de x y quiere maximizar el valor de f(x,y) mientras que otro agente varía el valor de y para minimizar el mismo f(x,y)) .

Referencias

Referencias e información de imágenes pulsando en ellas.