Cuádrica

---

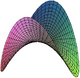
Cuádrica

Una cuádrica es una superficie determinada por una ecuación de segundo grado, es decir de la forma $P(x_{1},x_{2}...x_{n})=0\$ donde P es un Polinomio de segundo grado en las coordenadas $x_{1},x_{2}...x_{n}\$.

Cuando no se precisa, es una superficie del espacio tridimensional real usual, en un sistema de coordenadas ortogonal y unitario, y las coordenadas se llaman x, y y z. Son los matemáticos griegos de la antigüedad que inauguraron el estudio de las cuádricas (sin emplear las ecuaciones) con el cono (una cuádrica) y sus secciones, que son las cuádricas en el plano bidimensional.

La definición puramente algebraica de las cuádricas tiene el defecto de incluir casos sin interés geométrico y sin vínculo con el tema. Ejemplos:

• La ecuación
  $x^{2}+y^{2}+z^{2}+2xy+2yz+2xz=0\$
  es de segundo grado pero, mirando bien, se escribe
  $(x+y+z)^{2}=0\$
  lo que equivale a $x+y+z=0\$, ecuación de primer grado que corresponde a un plano, superficie que no tiene las propiedades relacionadas con el segundo grado. Más generalmente se descartan todos los polinomios de segundo grado que son cuadrados.

• La ecuación $x+y-xz-yz=0\$, de segundo grado también, se factoriza en $(x+y)\cdot (1-z)=0$ y equivale a x + y = 0 ó 1 – z = 0 ; la superficie es la reunión de los planos y = - x y z = 1 y recibe el nombre de cuádrica degenerada.

• Tampoco se suele aceptar ecuaciones como
  $x^{2}+y^{2}+z^{2}=-1\$
  que corresponde al conjunto vacío,
  $(x-1)^{2}+(y-2)^{2}+(z-3)^{2}=0\$
  que da un punto, (1; 2; 3), ni
  $(x-2)^{2}+(y+z)^{2}=0\$
  que da una recta, definida por x = 2 y z = - y; porque no tienen la dimensión esperada (dos) para ser una superficie.

Tipos de cuádricas

Descartados todos estos casos, las cuádricas caen en una de las categorías siguientes: (A→B significa que B es un caso particular de A):

Elipsoide	→	elipsoide de revolución (esferoide)   →   esfera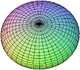
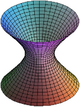
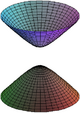
Hiperboloide	→     →	hiperboloide de una hoja hiperboloide de dos hojas
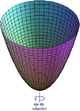
Paraboloide	→     →	paraboloide elíptico   →   paraboloide de revolución paraboloide hiperboloico
Cono (de base elíptica)	→	cono de revolución
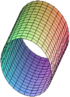
Cilindro	→     →     →	cilindro de revolución cilindro hiperboloico cilindro parabólico

Se puede concebir el cono como el caso límite entre los hiperboloides de una y de dos hojas.

En los cilindros, solamente dos variables intervienen, la tercera no aparece en la ecuación.

Método de clasificación

La clasificación de las formas es una rama importante de la geometría, y se hace de forma rigurosa. El criterio escogido aquí es el siguiente: dos cuádricas pertenecen a la misma categoría cuando se puede pasar de la una a la otra mediante un cambio de sistema de coordenadas. Geométricamente corresponde a una isometría (traslación y rotación) seguida de «estirados» x → a·x, y → b·y, z → c·z.

A partir de la ecuación general vamos a encontrar los distintos tipos de cuádricas.

La ecuación general es:

$ax^{2}+by^{2}+cz^{2}+dxy+exz+fxz+gx+hy+iz+j=0\$

, con los seis primeros coeficientes no simultáneamente nulos (sino sería del primer grado).
Esto se puede escribir matriciamente así:

${}^{t}XAX+BX+j=0\$

con:

$A={\begin{pmatrix}a&d/2&e/2\\d/2&b&f/2\\e/2&f/2&c\end{pmatrix}}$ una matriz simétrica, $B={\begin{pmatrix}g&h&i\end{pmatrix}}$ un vector línea, y $X={\begin{pmatrix}x\\y\\z\end{pmatrix}}$ un vector columna.

En efecto:

${\begin{pmatrix}x&y&z\end{pmatrix}}{\begin{pmatrix}a&d/2&e/2\\d/2&b&f/2\\e/2&f/2&c\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}+{\begin{pmatrix}g&h&i\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}=ax^{2}+by^{2}+cz^{2}+dxy+exz+fxz+gx+hy+iz$

Por ser simétrica, la matriz A puede diagonalizarse, es decir que existe una base en la que A se escribe $D={\begin{pmatrix}\alpha &0&0\\0&\beta &0\\0&0&\gamma \end{pmatrix}}$

Concretamente

$A={}^{t}RDR\$

, donde R es la matriz que realiza el cambio de base (es inversible, de inverso R⁻¹)
La ecuación matricial inicial

${}^{t}XAX+BX+j=0\$

se reescribe:

${}^{t}X^{t}RDRX+BR^{-1}RX+j=0\$

Es decir:

${}^{t}(RX)D(RX)+BR^{-1}(RX)+j=0\$

Sea

$X'={\begin{pmatrix}x'\\y'\\z'\end{pmatrix}}=RX$

el vector posición en la nueva base, $E={\begin{pmatrix}e_{1}&e_{2}&e_{3}\end{pmatrix}}=BR^{-1}$ el valor de B en la nueva base. La ecuación anterior se escribe:

${}^{t}X'DX'+EX'+j=0\$

es decir:

${\begin{pmatrix}x'&y'&z'\end{pmatrix}}{\begin{pmatrix}\alpha &0&0\\0&\beta &0\\0&0&\gamma \end{pmatrix}}{\begin{pmatrix}x'\\y'\\z'\end{pmatrix}}+{\begin{pmatrix}e_{1}&e_{2}&e_{3}\end{pmatrix}}{\begin{pmatrix}x'\\y'\\z'\end{pmatrix}}+j=\alpha {x'}^{2}+\beta {y'}^{2}+\gamma {z'}^{2}+e_{1}x+e_{2}y+e_{3}z+j=0$

Se ha logrado así hacer desaparecer los términos rectángulos xy, xz e yz.

• Si α, β y γ son todos no nulos, se puede hacer desaparecer los términos lineales (de primer grado) mediante la traslación
  $x''=x'+{\frac {e_{1}}{2\alpha }},\ y''=y'+{\frac {e_{2}}{2\beta }},\ z''=z'+{\frac {e_{3}}{2\gamma }}$
  se obtiene finalmente:
  $\alpha {x''}^{2}+\beta {y''}^{2}+\gamma {z''}^{2}=K\$
  con K una constante (
  $K={\frac {{E_{1}}^{2}}{4\alpha }}+{\frac {{E_{2}}^{2}}{4\beta }}+{\frac {{E_{3}}^{2}}{4\gamma }}-J$
  ).
  • Si α, β y γ son del mismo signo entonces la superficie es un elipsoide cuando K tiene el mismo signo también. (Si K es del signo opuesto o nulo, se obtiene los casos descartados del conjunto vacío y del punto respectivamente).
  • Si α, β y γ no son del mismo signo entonces la superficie es un hiperboloide de una hoja si K tiene el signo minoritario, de dos hojas si K tiene el signo mayoritario, y es un cono cuando K es nulo. El cono corresponde por tanto al caso frontera entre los hiperboloides de una y de dos hojas.

• Si exactamente una de las tres constantes α, β y γ es nula, pongamos γ = 0, entonces no se puede hacer desaparecer la variable correspondiente (z) pero sí las demás, y se obtiene:
  $\alpha {x''}^{2}+\beta {y''}^{2}+e_{3}z'=L\$
  con L una constante.
  • Si e₃ ≠ 0, por la traslación
    $z''=z'-{\frac {L}{e_{3}}}$
    se obtiene:
    $\alpha {x''}^{2}+\beta {y''}^{2}+e_{3}z''=0\$
    , luego la superficie es un paraboloide, elíptico cuando α y β son del mismo signo, hiperbólico cuando α y β tienen signos opuestos.
  • Si e₃ = 0,
    $\alpha {x''}^{2}+\beta {y''}^{2}=L\$
    es la ecuación de un cilindro, elíptico cuando α y β son del mismo signo, hiperbólico cuando α y β tienen signos opuestos. L = 0 corresponde a casos descartados (un punto cuando α·β > 0, una unión de planos secantes cuando α·β < 0).

• Si exactamente dos de las tres constantes α, β y γ son nulas, digamos β = γ = 0, entonces hacemos desaparecer x' con una traslación, luego
  $\alpha {x''}^{2}+e_{2}y'+e_{3}z'=N\$
  con N una constante. Si e₂ y e₃ no son simultáneamente nulos, mediante una rotación en el plano (x", y") se obtiene la ecuación
  $\alpha {x''}^{2}+e_{4}y''=N\$
  luego
  $\alpha {x''}^{2}+e_{4}y'''=0\$
  gracias a una traslación, y la superficie es un cilindro parabólico (puesto que e₄ ≠ 0). El caso e₂ = e₃ = 0 corresponde a casos descartados (conjunto vacío cuando α·N < 0, unión de dos planos paralelos cuando α·N > 0, un sólo plano cuando N = 0).

En un sistema de coordenadas adecuado (ortogonal pero no normado a priori), las ecuaciones más sencillas de las cuádricas son esas:

Elipsoide	x² + y² + z² = 1
Hiperboloide	de una hoja: x² + y² = z² - 1 de dos hojas: x² + y² = z² + 1 Cono: x² + y² = z²
Paraboloide	elíptico: x² + y² = z hiperbólico: x² - y² = z
Cilindro	elíptico: x² + y² = 1 hiperbólico: x² - y² = 1 parabólico: x² = y

Generalización

Se generaliza la noción de cuádrica en tres dominios distintos: en el espacio proyectivo, en el espacio complejo, y en dimensiones superiores.

Una ecuación de tres variables define una superficie en el espacio complejo de dimensión 3: ℂ³. Tal superficie es localmente isomorfa a ℂ², por tanto a ℝ⁴, y la mente humana tiene muchos problemas en visualizar una superficie de dimensión real 4 en un espacio de dimensión real 6 (como ℂ³).

Para entender las cuádricas complejas, se puede estudiar sus secciones por espacios tridimensionales reales.

El método para clasificar las cuádricas complejas es básicamente el mismo que para las reales; la única diferencia es que los signos de los coeficientes carecen de importancia porque la propriedad i² = -1 permite modificarlos mediante cambios de sistema de coordenadas. Por ejemplo el elipsoide x² + y² + z² = 1 da, con el cambio z' = i·z (que corresponde a una rotación de ℂ³): x² + y² - z'² = 1 lo que corresponde a un hiperboloide.

La clasificación es por tanto la siguiente:

Elipsoide - Hiperboloide	x² + y² + z² = 1
Cono	x² + y² = z²
Paraboloide	x² + y² = z
Cilindro	elíptico o hiperbólico: x² + y² = 1 parabólico: x² = y