Elipse

Existen al menos tres maneras de definir las elipses:

1) Una elipse es una Sección cónica, es decir la intersección de un cono con un plano (con una condición sobre su inclinación)

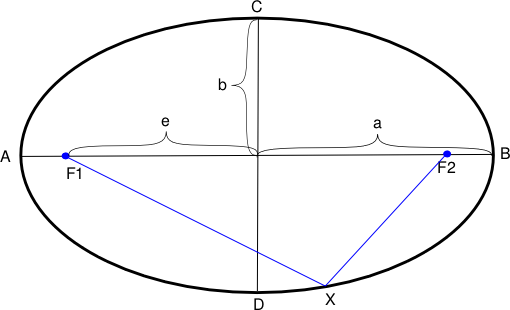
2) Sean F y F' dos puntos del plano, y d una longitud superior a FF'. La elipse de focos F y F', de parámetro d es el lugar geométrico de los puntos M del plano tales que FM + F'M = d.

3) En un sistema de coordenadas ortonormales, una elipse es el conjunto de puntos definidos por la ecuación:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Donde a > 0 y b > 0 son las semidistancias de los ejes de la elipse (a correponde al eje de las abscisas, b al de las Ordenadas). El origen O es la mitad del segmento [FF'].

Equivalencias

Cuando se define un mismo objeto de varias maneras distintas, es deseable demostrar que las distintas definiciones son equivalentes, o por lo menos dar indicios sobre como pasar de una a otra.

Después de ver como están vinculados los parámetros a, b, d y FF', se demostrará que las definiciones geométricas equivalen ambas a la definición algebraica, que es la más práctica para hacer cálculos.

A partir de los focos F y F', escojamos un sistema de coordenadas ortonormales así: el origen O es la mitand de [FF´], con F' del lado positivo. Sea c la semidistancia focal. Entonces F(-c, 0) y F'(c,0).

• Cuando el punto M está sobre el eje de las abscisas, por ejemplo en M₁, entonces d = FM₁ + F'M₁ = (FO + OM₁ ) + (OM₁ - OF') = 2·OM₁ = 2a, por definición de a. Entonces d/2 = a.
• Cuando M está sobre el eje de las ordenadas, por ejemplo en M₀, se puede aplicar el teorema de Pitágoras en los triángulos OFM₀ y OF'M₀, lo que da, con d = FM₀ + F'M₀ = 2FM₀ , (d/2)² = OM₂² + OF² = b² + c².

Igualando los dos resultados , se obtiene : a² = b² + c² (en la figura, a = 5 , b = 4 y c = 3, en cm). La excentricidad de la elipse es ε = c/a.
Luego, F'M + FM = k equivales a:

${\sqrt {(x-c)^{2}+y^{2}}}+{\sqrt {(x+c)^{2}+y^{2}}}=2a$

Tomando cuadrados:

$(x-c)^{2}+y^{2}+(x+c)^{2}+y^{2}+2{\sqrt {(x-c)^{2}+y^{2}}}{\sqrt {(x+c)^{2}+y^{2}}}=4a^{2}$

Aislando las raíces y dividiendo por dos:

${\sqrt {(x^{2}+c^{2}-2cx+y^{2})(x^{2}+c^{2}+2cx+y^{2})}}=2a^{2}-(x^{2}+y^{2}+c^{2})$

Factorizando y simplificando con $c^{2}=a^{2}-b^{2}$

${\sqrt {\left(x^{2}+c^{2}+y^{2}\right)^{2}-\left(2cx\right)^{2}}}=a^{2}+b^{2}-x^{2}-y^{2}$

Tomando de nuevo los cuadrados:

$\left(x^{2}+c^{2}+y^{2}\right)^{2}-\left(2cx\right)^{2}=\left(a^{2}+b^{2}-x^{2}-y^{2}\right)^{2}$

Transponiendo:

$\left(x^{2}+c^{2}+y^{2}\right)^{2}-\left(a^{2}+b^{2}-x^{2}-y^{2}\right)^{2}=\left(2cx\right)^{2}$

Factorizando:

$(c^{2}+a^{2}+b^{2})(2x^{2}+2y^{2}+c^{2}-a^{2}-b^{2})=\left(2cx\right)^{2}$

Sustituyendo $c^{2}=a^{2}-b^{2}$:

$2a^{2}(2x^{2}+2y^{2}-2b^{2})=4c^{2}x^{2}$

Simplificando por 4:

$a^{2}(x^{2}+y^{2}-b^{2})=c^{2}x^{2}$

Desarrollando y tranponiendo:

$(a^{2}-c^{2})x^{2}+a^{2}y^{2}=a^{2}b^{2}$

Sustituyendo nuevamente $c^{2}=a^{2}-b^{2}$:

$b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}$

Finalmente, dividiendo por $a^{2}b^{2}$

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Acabamos de demostrar que las definiciones 2 y 3 son equivalentes.

Queda por demostrar que lo son también las 1 y 3. Esto se hace traduciendo la primera definición a un lenguaje algebraico.
La cónica de referencia es la que tiene como ecuación, en el espacio: x² + y² = z², en un sistema de coordenadas ortonormales.
Un plano no vertical tendrá como ecuación z = αx + βy + γ. Para que la sección sea una elipse y no una hipérbola o una parábola, es preciso que su inclinación con relación al plano horizontal sea menor que la del borde de la cónica (la recta que genera la cónica por rotación). Esto equivale a: |α| < 1 y |β| < 1. Este resultado se obtiene mirando el plano y la cónica en los planos x = 0 e y = 0. Mediante una rotación, lo que no cambia la naturaleza de la forma, es posible imponer que uno de los factores α o β sea nulo (equivale a buscar un vector horizontal en el plano). Entonces α·β = 0.

La intersección tiene como ecuación:

$x^{2}+y^{2}=(\alpha x+\beta y+\gamma )^{2}$

Al desarollarla, obtenemos:

$(1-\alpha ^{2})\cdot x^{2}+(1-\beta ^{2})\cdot y^{2}=\delta x+\epsilon y+\zeta$

Se ha aislado los terminos de segundo grado. Como α·β = 0, el término en x·y, α·β·x·y desaparece.

Lo importante aquí es que los factores $(1-\alpha ^{2})$ y $(1-\beta ^{2})$ son ambos estrictamente positivos. Si fuesen de signo contrario, se trataría de una hipérbola, y si uno fuese nulo, de una parábola.

Con una translación (por un cambio de variable) se hace desaparecer la términos de primer grado:

$(1-\alpha ^{2})\cdot X^{2}+(1-\beta ^{2})\cdot Y^{2}=\omega$

Si ω = 0 se obtiene un conjunto reducido a un punto; es una sección de la cónica, de hecho es una elipse (y un círculo) que corresponde (tomando alguna libertad) a a = 0 y b = 0 en nuestra ecuación reducida. No vale la pena cambiar de ecuación para incluir este caso sin interés.

Si ω > 0, se cambia de escala multiplicando los vectores unitarios por ${\sqrt {\omega }}$ lo que divide las coordenadas por el mismo factor, y obtenemos:

$(1-\alpha ^{2})\cdot X^{2}+(1-\beta ^{2})\cdot Y^{2}=1$,

que equivale a la tercera definición, con:

$a={\frac {1}{\sqrt {1-\alpha ^{2}}}}$

$b={\frac {1}{\sqrt {1-\beta ^{2}}}}$

La dos definiciones geométricas equivalen a la algebraica, y por lo tanto son equivalentes entre sí.

Propiedades

• Ecuación paramétrica: La elipse anterior tiene como ecuaciones paramétricas

$x=a\cdot \cos \theta$

$y=b\cdot {\mbox{sen}}\theta$

con θ describiendo el intervalo [0;2π]

• La tangente a la elipse en el punto M (x₀, y₀ ) admite como ecuación:

${\frac {x\cdot (x-x_{0})}{a^{2}}}+{\frac {y\cdot (y-y_{0})}{b^{2}}}=0$

que se escribe también:

${\frac {x\cdot x_{0}}{a^{2}}}+{\frac {y\cdot y_{0}}{b^{2}}}=1$

(que se obtiene con el método de desdoblamiento de las variables)

• El área interior a la elipse es π·a·b.

• En mecánica, un cuerpo sometido a la atracción de otro (tomado como punto de referencia, es decir considerado fijo) y que gira a su alrededor, describe una órbita elíptica (ver Leyes de Kepler). Uno de los focos de la elipse coincide con el cuerpo atractor (El otro foco no contiene cuerpo alguno). La excentricidad de la trayectoria depende de las condiciones iniciales es decir de la historia del cuerpo.

Referencias

Referencias e información de imágenes pulsando en ellas.