Polígono

---

Polígono

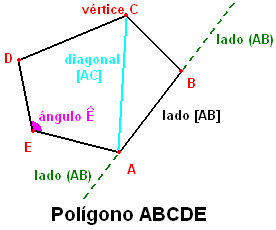
Un polígono (del griego πoλυς "polys": varios, muchos, numerosos, y γωνια "gônia": ángulo) es una figura geométrica plana limitada por tres o más líneas rectas que se cortan en sus vértices.

Los lados son las rectas que pasan por dos vértices adyacentes o los segmentos que los unen, según el contexto.

Una diagonal es un segmento que une dos vértices no adyacentes, es decir que no pertenecen al mismo lado.

A cada vértice le corresponde un ángulo "interior" definido por los dos lados que convergen en el vértice.

Según el número de vértices, n, los polígonos reciben apelaciones específicas:

nº de vértices	3	4	5	6	7	8	9	10
nombre especial	triángulo	cuadrilátero	pentágono	hexágono	heptágono	octágono	nonágono	decágono

Propiedades

Ángulos

La suma de los ángulos, $a_{n}$, de un polígono de n vértices es:

$a_{n}=(n-2)\cdot \pi$ radianes $=(n-2)\cdot 180$ grados

Esto se demuestra por inducción:

• Para iniciar la inducción se constata que es cierto para el triángulo porque sus ángulos suman 180°,
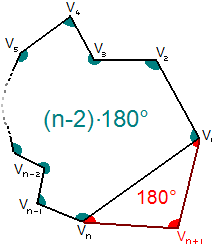
• luego se observa que un polígono cualquiera de $n+1$ vértices (V₁, V₂ ..., V_n+1, $n>3$), siempre se puede descomponer en uno de n vértices (V₁, V₂ ..., V_n), con sus ángulos sumando $(n-2)\cdot \pi$ radianes por la hipótesis de inducción, y un triángulo (V₁, V_n, V_n+1) cuyos ángulos suman π radianes.

La suma total es $(n-2)\cdot \pi +\pi =(n-1)\cdot \pi$ que corresponde a la fórmula con $n+1$ vértices.

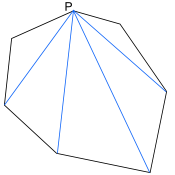
Llegamos al mismo resultado considerando que en un polígono de n lados podemos trazar (n-2) diagonales desde un mismo vértice, con lo que lo descomponemos en (n-2) triángulos. Puesto que para cada triángulo la suma total de sus ángulos vale 180º, obtenemos que los ángulos del polígono suman $a_{n}=(n-2)\cdot 180^{\circ }$

Convexidad

Un polígono es convexo si y sólo si ninguno de sus ángulos es mayor que 180°. En este caso, el polígono es una intersección de n semiplanos (n sigue siendo el número de vértices, y también el de aristas), lo que permite, en un determinado sistema de coordenadas, caracterizar al polígono por un sistema de inecuaciones.

Diagonales

El número de diagonales, d, de un polígono de n lados es:

$d={\frac {n\cdot (n-3)}{2}}$

Por ejemplo, un triángulo no tiene diagonales (si $n=3$ entonces $d=0$), un cuadrilátero tiene dos (si $n=4$ entonces $d=2$), y un pentágono cinco.

La prueba es sencilla: cada vértice (son n) conecta vía una diagonal con todas las demás salvo ella misma y sus dos vecinas (son entonces $n-3$ destinos posibles). Esto daría $n\cdot (n-3)$ diagonales, sin embargo una misma diagonal es contada dos veces, porque por ejemplo la diagonal [AC] es también la diagonal [CA], por tanto hay que dividir por dos el último valor.

Clasificación

Se distinguen los polígonos regulares de los que no lo son.

Referencias

Referencias e información de imágenes pulsando en ellas.