Inscríbete y crea tu propia colección de obras y artículos
Mediatriz
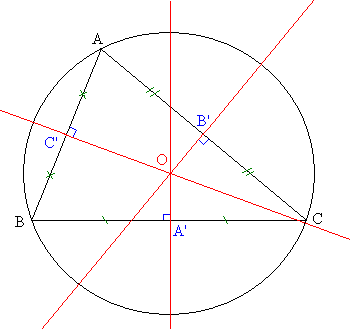
La mediatriz de un segmento [AB] es la recta de los puntos (del plano) equidistantes de A y B.
Por razones de simetría, la mediatriz corta el segmento [AB] por su mitad y perpendicularmente.
Teorema:
En un triángulo ABC, las mediatrices de los tres lados se cortan en un único punto, (O en la figura) que es centro del círculo circunscrito al triángulo.
Prueba:
- Dos lados nunca son paralelos, por consiguiente tampoco lo son las mediatrices, que hacen ángulos rectos con ellos.
- Sea O el punto de intersección de la mediatriz de [AB] con la de [BC]. Luego OA = OB, pero también OB = OC. Estas dos igualdades implican que OA = OC, es decir que O también pertenece a la tercera mediatriz. Por lo tanto las tres son concurrentes.
- El punto O, al ser equidistante de los tres vértices (OA = OB = OC) es centro de un círculo que pasa por ellos tres.
Referencias
 |
 |
