Inscríbete y crea tu propia colección de obras y artículos
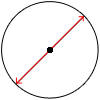
Diámetro
El diámetro de una circunferencia es el segmento que pasa por el centro y sus extremos son puntos de ella. Es la máxima cuerda (segmento entre dos puntos de la circunferencia) que se encuentra dentro de una circunferencia, o en un círculo. El diámetro de una esfera es el segmento que pasando por el centro, tiene sus extremos en la superficie de esta.
Diámetro de un círculo
Euclides de Alejandría define así el diámetro en sus Elementos, libro I, definición 17:
"Un diámetro de un círculo es una recta cualquiera que pasa por el centro y que acaba en ambas direcciones en la circunferencia del círculo; esta línea recta también divide el círculo en dos partes iguales"
Euclides de Alejandría, Elementos, libro I, definición 17.
La relación entre la longitud de la circunferencia y su diámetro es una constante que se conoce como π (pronunciado "pi"), y su valor se encuentra próximo a 355/113 (ó 3,14159...)
Como en una circunferencia el diámetro mide el doble del radio, la longitud de la circunferencia respecto su radio r es: 2πr.
Símbolo de diámetro
En ingeniería y otras áreas técnicas, el símbolo o variable para el diámetro es similar en tamaño y diseño a ø. Unicode ofrece el carácter 8960 (hexadecimal 2300) para el símbolo, el cual puede ser codificado en páginas web HTML como ⌀ o ⌀. Sin embargo, una adecuada presentación de dicho carácter es improbable en casi todas las situaciones ya que la mayoría de tipos de letra no lo tienen incluido. (El navegador muestra ⌀ y ⌀ en el tipo de letra actual). Casi siempre ø es aceptable, obtenido en Windows presionando la tecla [Alt] mientras se ingresa 0 2 4 8 en el Teclado numérico.
Es importante no confundir el símbolo de diámetro (ø) con el símbolo de Conjunto vacío, similar pero en mayúsculas (Ø). El diámetro es a veces llamado también phi (pronunciado "fi"), aunque esto parece provenir del hecho que Ø y ø se parecen a Φ y φ, la letra phi del alfabeto griego.
Se llega a abreviar como: día. o D.
Referencias
 |
 |
