Bisectriz

La bisectriz de un ángulo o un sector angular es la recta que divide el ángulo en dos partes iguales.

propiedad : los puntos de la bisectriz son equidistantes de los dos lados (rectas) del ángulo.

Recíprocamente, dos rectas, al cruzarse, forman cuatro ángulos, opuestos dos por dos. Estos definen dos bisectrices. Los puntos equidistantes de las dos rectas son exactamente los puntos de las dos mediatrices. Este resultado se establece fácilmente al recordar que una bisectriz es un eje de simetría de su ángulo, y que las simetrías conservan las distancias.

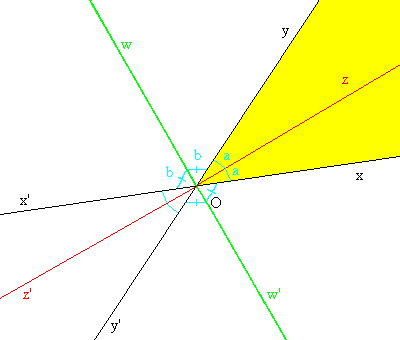
En la figura, la bisectriz interior al ángulo xOy (en amarillo) es (zz'), y la exterior es (ww'). Se cortan formando un ángulo recto. En efecto, si llamemos a la medida de xOz, y b la de yOw, observamos que 2a + 2b es la medida del ángulo xOx' , que es plano. Dividimos por 2: zOw mide a + b = ${\frac {\pi }{2}}$ radianes = 90º.

En un triángulo, los tres ángulos definen tres bisectrices (interiores).

Teorema: Las tres bisectrices del triángulo se cortan en un único punto, que es centro del círculo inscrito al triángulo.

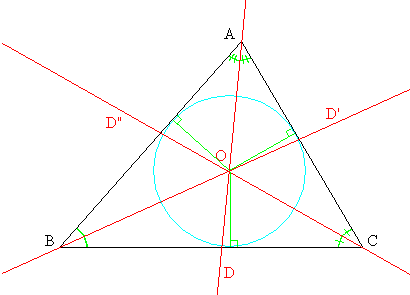
Prueba: Dos bisectrices del triángulo no pueden ser paralelas. Sea O la intersección de D y D' (ver figura). Como O pertenece a D, O es equidistante de las rectas (AB) y (AC). Como O pertenece a D', es equidistante de las rectas (AB) y (BC). Por transitividad de la igualdad, es equidistante de (AC) y (BC), y pertenece a la bisectriz (interior) del ángulo C, es decir a D". Al ser equidistante a los tres catetos, existe un círculo tangente a ellos y de centro O. (su radio es justamente la distancia común entre O y los catetos).